ทฤษฎีกราฟเบื้องต้น

ในเชิงคณิตศาสตร์ นิยาม “กราฟ” ดังนี้

บทนิยาม กราฟ G ประกอบด้วย เซตจำกัด 2 เซต คือ 1. เซตที่ไม่เป็นเซตว่างของจุดยอด(Vertex) แทนด้วยสัญลักษณ์ V(G) 2. เซตของเส้นเชื่อม (Edge) ที่เชื่อมระหว่างจุดยอด 
แทนด้วยสัญลักษณ์ E(G)

 ข้อสังเกต V(G) ≠ ∅ แต่ E(G) อาจเป็นเซตว่างได้

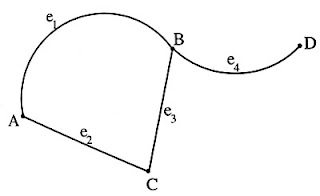
                     ตัวอย่างที่  กำหนดกราฟ G ดังรูป

จากกราฟ G ที่กำหนดให้ จะได้ว่า

                V(G) = {A, B, C, D}

                E(G) = {e₁, e₂, e₃, e₄}

บทนิยาม จุดยอด u และจุดยอด v ของกราฟ เป็นจุดยอดประชิด (Adjacent Vertices) ก็      ต่อเมื่อ มีเส้นเชื่อมระหว่างจุดทั้งสอง และเราเรียกจุดยอด u และ v ว่า จุดปลาย (End Point) ของเส้นเชื่อมนั้น  เส้นเชื่อม e ของกราฟ เกิดกับ (Incident) จุดยอด v ถ้าจุดยอด v เป็นจุดปลายจุดหนึ่งของเส้นเชื่อม

         
           ตัวอย่างที่  จากกราฟของตัวอย่างที่ 1 จะเห็นว่า

                 จุดยอด A และจุดยอด B เป็นจุดยอดประชิด

                 จุดยอด A และจุดยอด C เป็นจุดยอดประชิด

                 จุดยอด B และจุดยอด C เป็นจุดยอดประชิด

                จุดยอด C และจุดยอด D เป็นจุดยอดประชิด

           แต่ จุดยอด A และจุดยอด D ไม่เป็นจุดยอดประชิด      
                  จุดยอด B และจุดยอด D ไม่เป็นจุดยอดประชิด


หมายเหตุ

1. ในการเขียนแผนภาพของกราฟนั้น จะกำหนดตำแหน่งของจุดยอด ณ ตำแหน่งใดก็ได้ และจะลากเส้นเชื่อมของกราฟเป็นเส้นตรงหรือเส้นโค้งมีความยาวเป็นเท่าใดก็ได้
โดยที่เส้นที่ลากจะไม่ตัดกับตัวมันเอง และไม่ลากผ่านจุดยอดที่ไม่ใช่จุดยอดของเส้นนั้น เช่น กราฟต่อไปนี้ ถือว่าเป็นกราฟเดียวกัน

2. เส้นเชื่อมสองเส้นของกราฟ อาจลากตัดกันก็ได้ โดยที่จุดตัดของเส้นทั้งสองไม่ถือว่าเป็นจุดยอดของกราฟ

                  

                   บทนิยาม เส้นเชื่อมตั้งแต่ 2 เส้นที่เชื่อมระหว่างจุดยอดคู่เดียวกัน เรียกว่า 

                  เส้นเชื่อมขนาน(Parallel Edges)

                  เส้นเชื่อมที่เชื่อมจุดยอดเพียงจุดเดียว เรียกว่า วงวน (Loop)


ดีกรีของจุดยอด
    พิจารณากราฟต่อไปนี้

จุดยอด	จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด
a	2
b	4
c	4
d	2

          

   บทนิยาม ดีกรี (Degree) ของจุดยอด v ในกราฟ คือ จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด v
         ต่อไปจะเรียกจำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอดว่า ดีกรี ใช้สัญลักษณ์ deg v แทนดีกรีของจุดยอด v
           
             ตัวอย่างที่  กำหนดกราฟ ดังรูป

จากรูปจะได้ว่า deg a = 2

                   deg b = 1

                  deg c = 3

                  deg d = 4

ทฤษฎีบท

ให้ u₁, u₂, u₃, …, u)G(V เป็นจุดยอดทั้งหมดในกราฟ G จะได้ว่า
นั่นคือ ผลรวมของดีกรีของจุดยอดทุดจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ

พิสูจน์

       เนื่องจากเส้นเชื่อมแต่ละเส้นในกราฟเกิดกับจุดยอดเป็นจำนวน 2 ครั้ง ดังนั้นเส้นเชื่อมแต่ละเส้นจะถูกนับ 2 ครั้งในผลรวมของดีกรีของจุดยอดทุกจุด

นั่นคือ ผลรวมของดีกรีของจุดยอดทุกจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ

ข้อสังเกต

       ผลรวมของดีกรีของจุดยอดทุกจุดในกราฟเป็นจำนวนคู่เสมอ

บทนิยาม

       จุดยอดที่มีดีกรีเป็นจำนวนคู่ เรียกว่า จุดยอดคู่ (Even Vertex)

       จุดยอดที่มีดีกรีเป็นจำนวนคี่ เรียกว่า จุดยอดคี่ (Odd Vertex)
             

           ตัวอย่าง กำหนดกราฟ ดังรูป

จากรูปจะได้ว่า deg a = 2

                    deg b = 3

                   deg c = 0

                  deg d = 3

                  deg e = 2

ดังนั้น จุดยอด a, c และ e เป็นจุดยอดคู่    จุดยอด b และ d เป็นจุดยอดคี่

กราฟถ่วงน้ำหนัก (weight)
   
 บทนิยาม

     ค่าน้ำหนัก(weight) ของเส้นเชื่อม e ในกราฟ คือ จำนวนที่ไม่เป็นลบที่กำหนดไว้บนเส้นเชื่อม e

กราฟถ่วงน้ำหนัก(weight graph) คือ กราฟที่เส้นเชื่อมทุกเส้นมีค่าน้ำหนัก


                   ตัวอย่าง  กราฟต่อไปนี้เป็นถ่วงน้ำหนัก

กราฟออยเลอร์

        ปัญหาสะพานเคอนิกส์เบิร์ก มีอยู่ว่า ณ เมืองเคอนิกส์เบิร์กมีเกาะกลางแม่น้ำพรีเกล (Pregel)

จำนวน 2 เกาะ และมีสะพานที่เชื่อมระหว่างเกาะและเมืองดังรูปต่อไปนี้

        ชาวเมืองเคอนิกส์เบิร์กพยายามหาวิธีเดินข้ามสะพานให้ครบทุกสะพาน โดยที่ข้ามสะพานแต่ละสะพานเพียงครั้งเดียวและกลับมาที่จุดยอดเริ่มต้น 
         เลออนฮาร์ด ออยเลอร์ได้แปลงปัญหานี้ให้อยู่ในรูปกราฟ โดยให้อาณาบริเวณ A, B, C, D แทนด้วยจุดยอดของกราฟ และสะพานแต่ละพานแทนด้วยเส้นเชื่อมของกราฟ 

บทนิยาม

       วงจรออยเลอร์(Euler trail) คือ รอยเดินซึ่งผ่านจุดยอดทุกจุดและเส้นเชื่อมทุกเส้นของกราฟ

ทฤษฎีบท ให้ G เป็นกราฟเชื่อมโยง จะได้ว่า

G เป็นกราฟออยเลอร์ ก็ต่อเมื่อ จุดยอดทุกจุดของ G มีดีกรีเป็นจำนวนคู่

               กราฟที่มีวงจรออยเลอร์ เรียกว่า กราฟออยเลอร์ (Eulerian graph)

ตัวอย่าง กราฟต่อไปนี้เป็นกราฟออยเลอร์

ทฤษฎีบท ให้ G เป็นกราฟเชื่อมโยง จะได้ว่า G เป็นกราฟที่มีรอยเดินออยเลอร์ ก็ต่อเมื่อ G มีจุดยอดที่เป็นดีกรีเป็นจำนวนคี่ไม่เกิน 2 จุด ยิ่งไปกว่านั้นจุดยอดที่เป็นจำนวนคี่เหล่านั้นจะเป็นจุดเริ่มต้นและจุดปลายของรอยเดินออยเลอร์

ปัญหาหนี่งที่ดูคล้ายกับปัญหาวงจรออยเลอร์ คือปัญหาการหาวิถีในกราฟที่ไม่ใช้จุดยอดซ้ำกันยกเว้นจุดเริ่มต้นและจุดสิ้นสุดต้องเป็นจุดเดียวกัน ซึ่งก็คือ วัฎจักรและวัฎจักรนี้ผ่านครบทุกจุดยอดในกราฟนี้ จะเรียกวัฎจักรนี้ว่า วัฎจักรแฮมิลตัน

         ถ้า G มีวัฎจักรแฮมิลตัน จะเรียก G ว่าเป็นกราฟแฮมิลตัน(Hamiltonian graph)

ต้นไม้  

ต่อไปเราจะศึกษากราฟที่มีลักษณะพิเศษชนิดหนึ่ง เรียกว่า ต้นไม้ ซึ่งมีบทบาทสำคัญในการศึกษาทฤษฎีกราฟ และในการประยุกต์ทางด้านต่างๆ เช่น โครงสร้างข้อมูลในวิชาคอมพิวเตอร์ การศึกษาโครงสร้างทางเคมีของสารประกอบไฮโดร์คาร์บอน หรือในการออกแบบวงจรไฟฟ้าและอิเล็กทรอนิกส์

           บทนิยาม ต้นไม้ (tree) คือ กราฟเชื่อมโยงที่ไม่มีวัฏจักร
              ตัวอย่าง พิจารณากราฟต่อไปนี้

  

ลักษณะเฉพาะของต้นไม้
ทฤษฎีบท
            1. ให้ T เป็นกราฟที่ไม่มีวงวน กราฟ T เป็นต้นไม้ ก็ต่อเมื่อ จุดยอด 2 จุดใดๆ ใน T เชื่อมโยงกันได้ด้วยวิถีเพียงวิถีเดียว 
            2. ให้ T เป็นกราฟที่มีจำนวนจุดยอดเป็น n จุด กราฟ T เป็นต้นไม้ ก็ต่อเมื่อ กราฟ T ไม่มีวัฏจักร และมีเส้นเชื่อม n – 1 เส้น 
            3. ให้ T เป็นกราฟที่มีจำนวนจุดยอดเป็น n จุด กราฟ T เป็นต้นไม้ ก็ต่อเมื่อ กราฟ T เป็นกราฟเชื่อมโยงและมีเส้นเชื่อม n – 1 เส้น
            4. ถ้า T เป็นต้นไม้ที่มีจำนวนจุดยอดอย่างน้อย 2 จุด แล้ว กราฟ T จะมีดีกรี 1 อย่างน้อย 2 จุด

ที่มา

https://sites.google.com/site/graphmath101/home

https://www.google.co.th/search?q=%E0%B8%97%E0%B8%A4%E0%B8%A9%E0%B8%8E%E0%B8%B5%E0%B8%81%E0%B8%A3%E0%B8%B2%E0%B8%9F%E0%B9%80%E0%B8%9A%E0%B8%B7%E0%B9%89%E0%B8%AD%E0%B8%87%E0%B8%95%E0%B9%89%E0%B8%99&bav=on.2,or.r_cp.r_qf.&bvm=bv.51495398,d.aGc,pv.xjs.s.en_US.M4-36_38X9A.O&biw=1366&bih=667&um=1&ie=UTF-8&hl=th&tbm=isch&source=og&sa=N&tab=wi&ei=WCAnUoLGJqaTigeYp4H4Cw#imgdii=_

http://www.youtube.com/watch?v=2V03gZ450qw

  วันที่ 5 กันยายน 2556